Dr. Dmitri Babikov

(Funded by the National Science Foundation)

Inelastic scattering processes play important roles in a broad variety of chemical and physical phenomena. For example, they are crucial for quantitative interpretation of molecular spectra observed in astrochemical environments, modeling atmospheric chemistry, development of cooling and trapping techniques at ultracold temperatures and description of thermalization of enthalpy released by chemical bonds in combustion. Calculations of inelastic cross sections are usually carried out using quantum scattering codes such as MOLSCAT but the full-quantum scattering calculations, physically indispensable and computationally affordable at low temperatures, become prohibitively demanding at higher temperatures and/or for heavier (polyatomic) molecules and quenchers. It is important to realize that at such conditions the intermolecular degrees of freedom can be treated classically. Computationally powerful and physically appropriate method for description of inelastic scattering can be formulated if the classical trajectory treatment of scattering is interfaced with quantum treatment of rotation (and/or vibration) in a self-consistent way, which allows energy exchange between external and internal degrees of freedom, but keeps total energy conserved.

The idea of such mixed quantum/classical theory (MQCT) is not entirely new, but it has never been fully developed to the level of a predictive computational tool. In a series of recent papers we presented and tested, using a model system and several real molecules, the general and fully-coupled version of MQCT, formulated in both laboratory-fixed and body-fixed reference frames. The level of agreement between MQCT and full-quantum calculations is very encouraging, if not to say exciting. We want to stress that MQCT was applied without any adjustments which makes this general theory an excellent candidate for the “black box” utilization in a broad spectrum of applications, even by non-expert users. The computer code is simple and calculations are highly affordable. Furthermore, calculations with different impact parameters are entirely independent, which makes this method intrinsically parallel: one can easily spread MQCT trajectories onto hundreds of processors with zero communication overlap. The results obtained so far indicate that MQCT is more accurate for heavier masses, at higher collision energies and smaller spacings between quantized states (energy quanta). Importantly, in this regime the full-quantum method becomes computationally costly, while the MQCT calculations become very affordable.

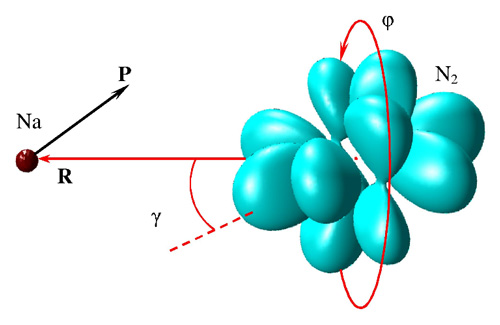
Figure 11: Schematic of MQCT calculations for Na + N₂ in the BF reference frame. The quencher atom (treated classically) scatters off the ro-vibrational wave function of the molecule.  Coordinates are defined in the text. Initial position of the quencher is on polar axis. Incident direction of its momentum vector P is determined by impact parameter.

Relevant Publications

1. D. Bostan, B. Mandal, C. Joy, M. Zoltowski, F. Lique, J Loreau, E Qiuntas-Sanchez, A Batista-Planas, R. Dawes, and D. Babikov “Mixed quantum/classical calculations of rotationally inelastic scattering in the CO + CO system: a comparison with fully quantum results” Phys. Chem. Chem. Phys. 26, pp. 6461 – 7242, 2024

2. C. Joy, B. Mandal, D. Bostan and D. Babikov “Mixed Quantum/Classical Theory for Rotational Energy Exchange in Symmetric-Top-Rotor + Linear-Rotor Collisions and a Case Study of ND3 + D2 System” Phys. Chem. Chem. Phys. 25, pp. 17287 – 17299, 2023. 
2. D. Bostan, B. Mandal, C. Joy and D. Babikov “Description of Quantum Interference Using Mixed Quantum/Classical Theory of Inelastic Scattering” Phys. Chem. Chem. Phys. 25, pp. 15683 - 15692, 2023. 
3. B. Mandal, and D. Babikov, “Rate coefficients for rotational state-to-state transitions in H2O + H2O collisions for cometary and planetary applications, as predicted by mixed quantum/classical theory” Astronomy & Astrophysics 671, A51, 2023. 
4. B. Mandal, C. Joy, D. Bostan, A. Eng and D. Babikov, “Adiabatic trajectory approximation – New general method in the toolbox of mixed quantum/classical theory for collisional energy transfer”, cover art, J. Phys. Chem. Lett. 14, 817−824, 2023. 
5. B. Mandal, C. Joy, A. Semenov and D. Babikov, “Mixed quantum/classical theory for collisional quenching of PAHs in the interstellar media” ACS Journal of Earth and Space Chemistry 6, 521-529, 2022.
6. D. Babikov and A. Semenov, “Recent Advances in Development and applications of Mixed Quantum/Classical Theory for Inelastic Scattering”, feature article (invited), J. Phys. Chem. A 120, pp. 319-331, cover art, 2016.  
7. A. Semenov and D. Babikov, “Mixed Quantum/Classical Theory for Molecule-Molecule Inelastic Scattering: Derivations of Equations and Application to N2 + H2 System”, invited paper for special issue “50 Years of Chemical Reaction Dynamics”, J. Phys. Chem. A 119, pp. 12329-2338, 2015. 
8. A. Semenov and D. Babikov, “Mixed quantum/classical approach for description of molecular collisions in astrophysical environments”, J. Phys. Chem. Lett. 6, 1854 (5 pages), 2015.

(Funded by the National Science Foundation)

The origin of anomalously large enrichments of stratospheric ozone in heavy isotopes has been a mystery for 30 years. The isotope ¹⁶O is dominant in the atmosphere, so that most oxygen molecules (O₂) consist of two ¹⁶O atoms. However, stratospheric ozone (O₃) is surprisingly observed to be heavily enriched in the isotope ¹⁸O relative to the atmospheric oxygen from which it’s formed. Careful experimental studies have shown that the recombination reaction that forms ozone,

O₂ + O →O₃,

is responsible for the effect. The recombination rates for various isotopic combinations differ by more then 50%, which is a remarkably large isotope effect taking into account small mass difference. We propose a clear explanation for the effect in terms of the energy transfer mechanism, where the metastable O₃* states of ozone are formed first and then stabilized by collisions with bath gas molecules M:

O₂ + O ↔ O₃* ↔ O + O₂,

O₃* + M → O₃ + M.

Sophisticated treatment is employed, which considers different metastable O₃* states as different species, with their energies and lifetimes obtained from accurate quantum scattering calculations. Population of the metastable O₃* states is found to build up and then decay back to O₂ + O through several possible channels. When different isotopes of oxygen are involved the channels become open at different energies due to the differences in quantum zero-point energies (ΔZPE) of different O₂ molecules.

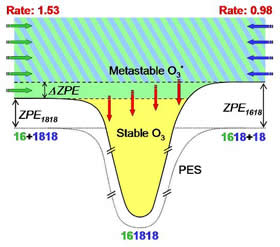
Figure 1: Schematic for recombination processes forming ¹⁶O¹⁸O¹⁸O isotopologue. The PES (dotted line), quantum ZPE for each entrance channels and the ΔZPE are shown (not to scale). The experimental formation rates (relative to the formation rate of ¹⁶O¹⁶O¹⁶O) for each channel are given at the top. Note one extra arrow in the ΔZPE energy range.

We found that the spectrum of metastable O₃* states is anomalously dense within the ΔZPE energy range, and these states are accessible only from the lower entrance channel. Also, the metastable states in the ΔZPE part of spectrum are stabilized very efficiently by collisions with M because they are energetically close to the bound O₃ states (see Fig. 1). Such processes significantly enhance the formation rates of ozone isotopologues through the lower energy channels. These findings have finally identified the molecular level origin of anomalous isotope effects observed in many experiments.

Current group activities involve further theoretical study of this and other quantum phenomena using the mixed quantum/classical method. Our purpose is to provide the most rigorous and complete description of the ozone forming reaction, including all associated isotope effects. Several other atmospheric reactions like

• NO+O → NO₂
• SO+O → SO₂
• S₂+S → S₃
• SH+H → SH₂

should exhibit a similar isotope effect. These reactions will be studied as well.

Relevant Publications

1. I. Gayday and D. Babikov, “Efficient method for an approximate treatment of Coriolis effect in the calculations of quantum dynamics and spectroscopy, with application to scattering resonances in ozone”, J. Phys. Chem. A 125, 5661–5669, 2021. 
2. D. Babikov, E. Grushnikova, I. Gayday and A. Teplukhin, “Four isotope-labeled recombination pathways of ozone formation”, Molecules 26, 1289 (21 pages), 2021.
3. I. Gayday, E. Grushnikova and D. Babikov, "Influence of the Coriolis effect on the properties of scattering resonances in symmetric and asymmetric isotopomers of ozone", Phys. Chem. Chem. Phys. 22, 27560 - 27571, 2020.
4. A. Teplukhin and D. Babikov, “Several levels of theory for description of isotope effects in ozone: Symmetry effect and Mass effect”, J. Phys. Chem. A 122, pp. 9177-9190, 2018.
5. A. Teplukhin, I. Gayday and D. Babikov, “Several levels of theory for description of isotope effects in ozone: Effect of resonance lifetimes and channel coupling”, J. Chem. Phys. 149, 164302 (13 pages), 2018.
6. M.V. Ivanov, D. Babikov, "On molecular origin of mass-independent fractionaltion of oxygen isotopes in the ozone forming recombination reaction" PNAS 110, 17708 (2013).

(supported by NSF, in collaboration with Los Alamos National Laboratory)

One of the long-thought applications of quantum computers is to simulate quantum systems, such as molecules and materials at the atomistic scale. Several algorithms were recently proposed for the calculations of molecular electronic structure (called quantum chemistry) using either gate-based quantum computers with only a few tens of qubits, such as Sycamore or IBM Q-machines, or using quantum annealers with a larger number of qubits, such as the D-Wave systems. Another essential component of chemical modeling is the propagation of the equations of motion for constituent atoms in time and space (e.g., along the reaction path), called molecular dynamics. For over 50 years, molecular dynamics simulations have played a pivotal role not only in guiding and analyzing experiments, but also as an interdisciplinary computational tool that is able to reach far beyond experimental conditions. Molecular dynamics is indispensable for a wide variety of research topics, but only a few attempts have been made so far to harness the power of quantum computing for the benefit of molecular dynamics simulations. 

We were among the first to explore this opportunity: A few years ago, we developed a new method (named QAE) to solve, on a quantum annealer, the problem of quantum vibrational dynamics as an eigenvalue problem, and, successfully implemented this algorithm using the actual quantum hardware (D-Wave annealer at LANL) to compute the vibrational states of O2 and O3 molecules. Later, this method was extended to compute the properties of quantum scattering resonances above the dissociation threshold (these metastable states play a central role in recombination reactions, such as ozone formation in the Earth’s stratosphere: O + O2 → O3). More recently, we developed another algorithm (named QDE, see Fig. 1) and successfully carried out the first ever molecular dynamics simulations on a quantum annealer, to propagate trajectories for the vibrational motion of atoms in the H2 molecule in various energy regimes, including large-amplitude anharmonic vibrations and bond breaking (i.e., dissociation reaction H2 + bath gas → H + H).

These pioneering proof-of-principle calculations are still restricted to small molecules, such as diatomic and triatomic systems, and are done in a hybrid quantum/classical fashion, when only a part of the overall algorithm is run on a present-day quantum device. However, they represent the first step toward the development of new algorithms, exploration of larger molecules, and modelling of more complex processes that may become possible using the last generation quantum computers, such as D-Wave’s Advantage.

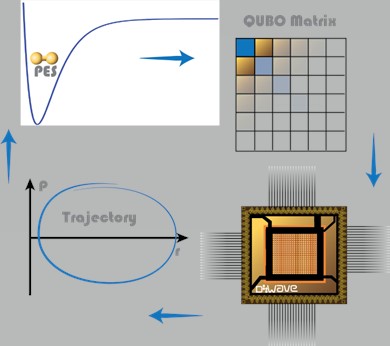
Fig. 1: Schematic representation of the workflow in our QDE algorithm for simulation of molecular dynamics on a quantum annealer, going from the potential function to QUBO matrix, to its minimization on quantum device, to making a timestep along the trajectory, and then repeating the cycle.

1. I. Gayday, D. Babikov, A. Teplukhin, B. K. Kendrick, S. M. Mniszewski, Y. Zhang, S. Tretiak, P. A. Dub, “Molecular dynamics on quantum annealers” Sci. Reports 12, 16824 (10 pages), 2022.
2. A. Teplukhin, B. Kendrick and D. Babikov, “Solving complex eigenvalue problems on a quantum annealer with applications to quantum scattering resonances”, Phys. Chem. Chem. Phys. 22, 26136-26144, 2020. 
3. A. Teplukhin, B. Kendrick and D. Babikov, “Calculation of molecular vibrational spectra on a quantum annealer”, J. Chem. Theory Comput. 15, 4555-4563, 2019. 
4. D. Shyshlov and D. Babikov, “Computational study of cold ions trapped in a double-well potential”, Mol. Phys. 117, 1912-1925, 2019.  

(Funded by the National Science Foundation)

We explore possibility of using the vibrational states of a polyatomic molecule for universal quantum computation. In this approach two vibrational eigenstates (typically, the ground and the first excited vibrational states) are used to represent |0› and |1› states of the quantum information unit, qubit. Different qubits are encoded into different normal vibration modes of a molecule and thus remain independent in the absence of external fields. All the quantum logics operations, starting with the simplest one-qubit flips and going to the more complicated multi-qubit gates, can be applied to such a vibrational register using infrared laser pulses carefully prepared (shaped) in order to induce only the desired vibrational transitions while suppressing the interfering ones. Such an optimal pulse shape can be either predicted theoretically using the optimal control theory or derived experimentally using the adaptive learning algorithms.

According to standard convention the first qubit is the control qubit and the second qubit is the target qubit. If the control qubit is in state |0›, the state of the target qubit remains intact but, if the control qubit is in the state |1›, the target qubit flips. The ground vibrational state, two overtones, and the combination state of the two normal vibration modes in naphthalene molecule (C10H8) are used to represent |00›, |01›, |10› and |11› states of two-qubit system, respectively.

In this project we try to model and understand how the properties of a molecule chosen to represent quantum bits, such as vibrational frequencies and anharmonicities, affect controllability of the qubit by sub-picosecond laser pulses. It appears that transitions to upper vibrational states. e.g., |2›, |3›, |4› etc., tend to interfere with transitions between the qubit states |0› and |1›. Resolving different transitions, suppressing unwanted ones while inducing the desired ones, is crucial for success of the method. The seemingly complicated picture can be rationalized in terms of general analytic relationships between the anharmonicity parameters and the frequencies. For example, for a two-qubit system these expressions represent planes in the three-dimensional anharmonicity parameter space. Only in the vicinity of these planes the interference effects are significant. Results of this work should help to choose a suitable candidate molecule for practical implementation of the quantum register of several vibrational qubits.

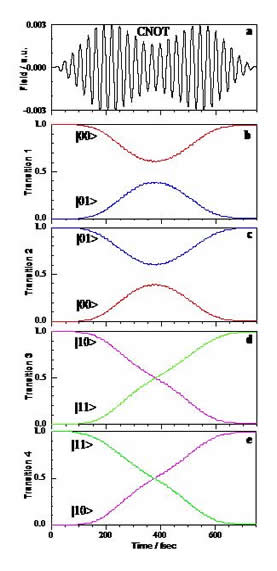
Figure 2:  Conditional NOT (CNOT) gate in a typical two-qubit system. a) Optimally shaped 750 fs laser pulse; b)-e) Population transfer between the qubit states during the pulse for four state-to-state transitions:

     (Transition 1);

     (Transition 2);

     (Transition 3);

     (Transition 4).

Relevant Publications

1. D. Shyshlov, D. Babikov, "Complexity and simplicity of optimal control theory pulses shaped for controlling vibrational qubits", J. Chem. Phys. 137, 194318 (2012).
2. L. Wang, D. Babikov, "Adiabetic coherent control in the anharmonic io trap: Proposal for the vibrational two-qubit system". Phys. Rev. A83, 052319 (2011).
3.  M. Zhao and D. Babikov, "Coherent and optimal control of adiabatic motion of ions in a trap", Phys. Rev. A 77, 012338 (2008).
4. M. Zhao and D. Babikov, "Anharmonic properties of the vibrational quantum computer", J. Chem. Phys. 126, 204102 (2007).
5. D. Babikov, “Accuracy of gates in a quantum computer based on vibrational eigenstates,” J. Chem. Phys. 121, 7577, (2004).
6. M. Zhao and D. Babikov, “Phase control in the vibrational qubit”, J. Chem. Phys. 125, 24105 (2006). 

(Supported by the Airforce Office of Scientific Research)

The previously unknown energetic form of nitrogen has been recently predicted theoretically and produced experimentally. This is a stable ring isomer of N₃ (having the form of an isosceles triangle) called cyclic-N₃ hereafter. Cyclic-N₃ was first detected in the UV photolysis experiments:

ClN₃+ hv  → Cl + N₃  

Experimental data showed that in addition to the already known weakly bound linear-N₃ isomer, there was another energetic form of N3, with energy about 1.35 eV above that of linear-N3. Thus, cyclic-N3 carries large amount of energy and is an interesting new candidate for technological applications in energy storage, high nitrogen explosives, and new propellants. It is worth mentioning that the nitrogen resources on our planet are practically limitless. Due to structural similarity the cyclic-N₃ (a radical) can probably be used as a precursor for creating tetrahedral N₄ (stable molecule) which then can be used as a powerful and clean monopropellant:

N₄   →  2N₂

Since this reaction produces only nitrogen molecules, the main component of atmospheric air, the exhaust gases present no environmental hazards and are indistinguishable from the ambient air.

All available experimental information for cyclic-N₃ is consistent with theoretical picture of this molecule; however, the final proof for the existence of cyclic-N₃ is yet to be made by means of high-resolution spectroscopy. Cyclic-N₃ is a Jahn-Teller molecule that exhibits a conical intersection between two of its potential energy surfaces at the D_3h (equilateral triangle) configuration. That conical intersection causes the equilibrium geometry to distort off the D_3h geometry. Further complication is due to the geometric phase effect, when the symmetry of electronic wave function changes six times as the vibrational wave function encircles the conical intersection.

In order to model the photoelectron spectrum of this molecule we have developed the PES for cationic species cyclic-N3+. We calculated all the vibrational states of cyclic-N3+ as well and finally derived the photo-electron spectrum of cyclic-N3 (see Fig. 4). This broad spectrum differs dramatically from that of the linear tri-nitrogen isomer, which has only one intense peak in this energy range due to similarity in the equilibrium structures of the neutral and ionized species. On the scale of Fig. 4 that single peak would appear at about 5680 cm-1. This difference should help to distinguish the two isomers simultaneously present in the experimental molecular beam.

We have developed an accurate ab initio the potential energy surface (PES) for cyclic-N₃, see Fig. 3, and carried out the state-of-the-art calculations of the vibrational energies and wave of functions cyclic-N₃. One important finding is an unusually large magnitude of the geometric phase effects in the cyclic-N₃: it is ~ 100 cm^-1 for the low lying vibrational states and exceeds 600 cm^-1 for several upper states. On average, this is almost two orders of magnitude larger than in other molecules. This unique example suggests a favorable path to experimental validation using infrared absorption spectroscopy.

Figure 3: A surface plot for stereographic projection of the cyclic-N3 PES. The value of the hyper-radius is fixed at 3.407 a.u. The conical intersection is seen at (x = 0, y = 0). The vertical axis gives energy in eV.

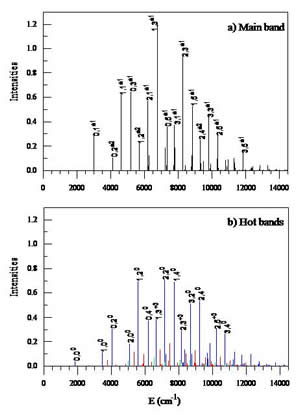
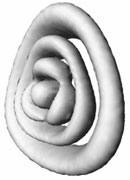
Figure 4: Theoretically predicted photoelectron spectra of cyclic-N₃.
a) Main band of transitions between the states of E-symmetry;
b) Hot bands of transitions between the states of A₁-symmetry (blue), A₂-symmetry (green), and E-symmetry (red). Final state labels in terms of polyads are given for several most intense peaks;
c) Vibrational wave function of one of cyclic-N₃⁺ states.

Relevant Publications

1. D. Babikov, "Perturbation theory treatment of pseudo-rotation in cyclic-N₃", J. Chem. Phys 134, 114305 (2011).
2. D. Babikov, B.K. Kendrick, "The infrared spectrum of cyclic-N₃: Theoretical prediction", J. Chem. Phys 133, 174310 (2010).
3. D. Babikov, V. A. Mozhayskiy and A. I. Krylov, “The photoelectron spectrum of elusive cyclic-N3 and characterization of the potential energy surface and vibrational states of the ion”, J. Chem. Phys. 125, 84306 (2006).
4. V. A. Mozhayskiy, D. Babikov and A. I. Krylov, “Conical and glancing Jahn-Teller intersections in the cyclic trinitrogen cation”, J. Chem. Phys. 124, 224309 (2006).
5. D. Babikov, B. Kendrick, P. Zhang, and K. Morokuma, “Cyclic-N3: II. Large geometric phase effects in the vibrational spectra”, J. Chem. Phys. 122, 44315 (2005).
6. D. Babikov, P. Zhang, and K. Morokuma, “Cyclic-N3: I. An accurate potential energy surface for the ground doublet electronic state up to the energy of the 2A2/2B1 conical intersection”, J. Chem. Phys. 121, 6743 (2004). 

(Supported by NERSC Center)

The semi-classical wavepacket method (SWP, also known as the Herman-Kluk propagator or as the initial value representation method) is a viable approach to theoretical description of many molecular processes including collisions, scattering and reaction dynamics. This method accounts for all features of the potential energy surface in a natural dynamic way, incorporates full dimensionality of the problem and avoids using sudden approximation. This is a time-dependent method based on propagating the ensemble of classical trajectories. In addition, every individual trajectory possesses phase and monodromy (stability) matrix, which allows different trajectories to interfere with each other and contribute coherently to the overall semiclassical wave function. All quantum effects appear as the result of this interference. It is well established that this approach describes the quantum zero-point energy, but much less is known about ability of the SWP method to reproduce quantum symmetry and characterize the quantum scattering resonances. These two quantum effects are known to be important for recombination reactions like one that forms ozone:

Thus, it would be instructive to test the validity of the SWP approach using a simplified problem relevant to the reaction dynamics. We have carried out such a methodological study: We applied the SWP method to describe quantum scattering resonances in an ozone-like two-body scattering system. We considered a simple model, where the internal structure of O₂ is neglected and the focus is on scattering resonances (metastable states) formed behind the centrifugal barrier due to the angular momentum of relative O₂+O motion. We considered all values of angular momentum required to calculate the converged rate of ozone formation and characterized every important resonance by its energy and lifetime. Overall, we looked at more than 80 resonances with lifetimes that evenly cover the range from 0.01 ps to 1000 ps. This certainly represents a thorough test of the SWP approach. To assess its accuracy we compared the SWP results against the data obtained using a fully quantum wavepacket propagation technique. We found that energies of the metastable states obtained using the SWP method are accurate to within 0.1 cm-1 and 2 cm^-1 for under-the-barrier and over-the-barrier states, respectively. The SWP lifetimes in the range 0.5 < τ < 100 ps are accurate to within 10%. Within the well region the SWP wave functions are identical to quantum ones. Only in the classically forbidden or in the barrier region the SWP method slightly underestimates tunneling, as can be seen from Fig. 5.

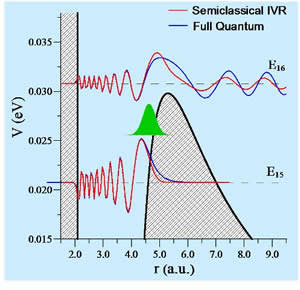
Figure 5: Barrier region of the J = 38 potential function. Initial semi-classical wave packet is placed at r0 = 4.64 a.u. Wave functions of under-the-barrier (v = 15) and over-the-barrier (v = 16) metastable states were calculated by propagating this initial wave packet, calculating the autocorrelation function and obtaining its Fourier transform. Shaded areas show the classically forbidden regions; the barrier top is at rtop = 5.29 a.u.

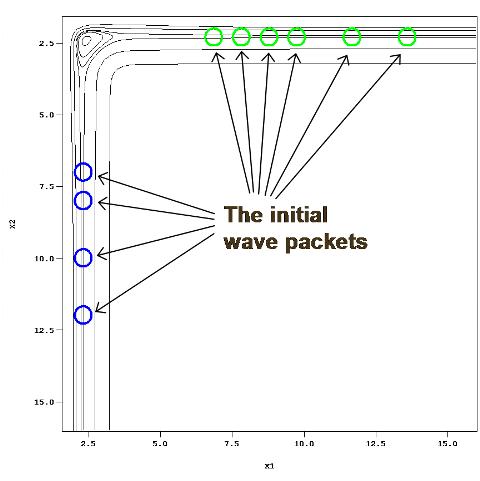
Figure 6: In order to capture the metastable states in the barrierless potential the initial wave packets should be placed far into the channels.

Animations:

• Wave packet dynamics in the mixed quantum-classical calculations. Download PowerPoint.

Relevant Publications

1. E. Vetoshkin and D. Babikov, "Semiclassical Wave Packet Treatment of Scattering Resonances: Application to the Delta Zero-Point Energy Effect in Recombination Reactions", PRL 99, 138301 (2007). 
2. E. Vetoshkin and D. Babikov, "Semiclassical wave packet study of anomalous isotope effect in ozone formation", J. Chem. Phys. 127, 154312 (2007). 
3. E. Vetoshkin and D. Babikov, “Semi-classical wave-packet study of ozone forming reaction”, J. Chem. Phys. 125, 24302, (2006). 
4. D. Babikov, R. B. Walker, and R. T Pack, “A quantum symmetry preserving semiclassical method”, J. Chem. Phys. 117, 8613, (2002). 
5. D. Babikov, F. Aguillon, M. Sizun and V. Sidis, “Fragmentation of Na2+ dimer ion in keV collisions with He: a coupled wave packet study”, Phys. Rev. A 59, 330, (1999). 

(collaboration with LCAM, Orsay, France)

Fragmentation of molecules or clusters by making them collide with atoms is a way of studying the dynamics of energy deposition and its subsequent distribution in polyatomic objects. Schematically, there are two main mechanisms by which collision-induced fragmentation can occur. The first mechanism involves energy or momentum transfer from the relative collisional motion to internal vibrational and rotational degrees of freedom of the molecule. If the transferred energy lies above the binding energy of an atom or a group of atoms in the molecule the latter may be freed and move apart. A particularly simple example of this mechanism is when the atomic projectile hits, in a close binary encounter, a specific atom or group of atoms in the molecule and kicks it out. This mechanism is called an impulsive mechanism. The second electronic mechanism involves excitation of a dissociative or predissociative electronic state of the molecule, which automatically entails its fragmentation.

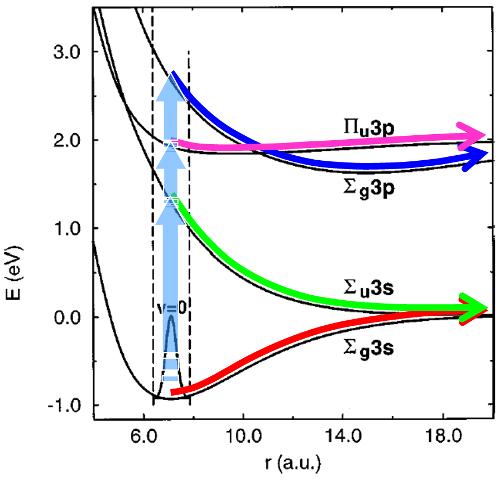
Figure 7: Two mechanisms of collision induced fragmentation of Na₂⁺. The impulsive mechanism occurs within the ground electronic state (red arrow), while the electronic mechanism proceeds through excitation of one or several dissociative electronic states (vertical arrows) with following fragmentation (green, purple and blue).

A step forward in the experimental investigation of collision-induced fragmentation has been made by combined time-of-flight and multiparametric coincidence techniques. Applied to the study of the following process

He + Na₂⁺ → He + Na + Na⁺

this experimental technique has made possible the complete measurement of all observables characterizing the collision-induced dissociation process, including the scattering angle x and the relative kinetic energy e of the fragments (see Fig. 8a). Although such achievements are highly challenging for theory, we were able to reproduce and explain every feature (see Fig. 8b) in the experimental “map” of doubly differential cross section σ(ε,x) for fragmentation. The electronic and impulsive mechanisms of fragmentation manifest themselves very clearly in our results. Our theoretical approach involved quasiclassical trajectory approximation for the relative motion of colliding partners and the quantum wavepacket treatment of the internal (vibrational) degree of freedom.

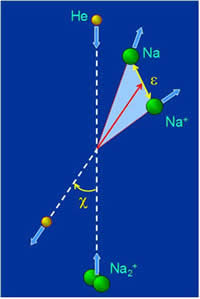
Figure 8: a) Center of mass scheme for the collision-induced fragmentation of Na₂⁺ in 1 keV collision with He target. b) Theoretically calculated doubly differential cross section σ(ε,χ) for fragmentation. Four structures on the σ(ε,χ) map correspond to four electronic states in Fig. 7 and correlate very closely with available experimental data.

Results of this work allowed detailed characterization of the fragmentation pathways for the multi-channel fragmentation of sodium triatomic:

   He + Na₃⁺ → He + Na + Na₂⁺

→ He + Na₂⁺ + Na

→ He + Na + Na + Na⁺

and for several larger sodium clusters as well.

Relevant Publications

1. D. Babikov, E. A. Gislason, M. Sizun, F. Aguillon, V. Sidis, M. Barat, J. C. Brenot, J. A. Fayeton and Y. J. Picard, “Dalitz plot analysis of three-body fragmentation of Na3+ excited by He impact”, J. Chem. Phys. 116,  4871, (2002). 
2. E. A. Gislason, D. Babikov, M. Sizun, F. Aguillon, V. Sidis, M. Barat, J. C. Brenot, J. A. Fayeton and Y. J. Picard, “Distribution of final electronic states following three-body fragmentation of Na3+ excited by He impact”, Chem. Phys. Let. 341, 568, (2001). 
3. D. Babikov, E. Gislason, M. Sizun, F. Aguillon and V. Sidis, “Fragmentation of Na3+ clusters by He impact: theoretical analysis of fragmentation mechanisms”, J. Chem. Phys. 112, 9417, (2000). 
4. D. Babikov, E. Gislason, M. Sizun, F. Aguillon and V. Sidis, “Theory for non-adiabatic multi-channel fragmentation of the Na3+ cluster ion following a collision with a He atom”, J. Chem. Phys. 112, 7032, (2000). 
5. D. Babikov, E. Gislason, M. Sizun, F. Aguillon and V. Sidis, “Fragmentation of Na3+ clusters by He impact: effect of initial cluster temperature on non-adiabatic phenomena”, Chem. Phys. Let. 316, 129, (2000). 
6. D. Babikov, M. Sizun, F. Aguillon and V. Sidis, “A theoretical description of multi-channel fragmentation of the Na3+ cluster-ion in collision with a He target”, Chem. Phys. Lett. 306, 226, (1999). 
7. M. Barat, J.C. Brenot, H. Dunet, J.A. Fayeton, Y. J. Picard, D. Babikov, M. Sizun and V. Sidis “Complete analysis of the Na3+ fragmentation in collision with He atoms”, Chem. Phys. Let. 306, 233, (1999). 
8. D. Babikov, F. Aguillon, M. Sizun and V. Sidis, “Fragmentation of Na2+ dimer ion in keV collisions with He: a coupled wave packet study”, Phys. Rev. A 59, 330, (1999). 

(Collaboration with Kevin Sanbonmatsu, Los Alamos)

Using the "Q Machine" supercomputer, Los Alamos computer scientists have created a molecular simulation of the cell's protein-making structure, the ribosome. The project, simulating 2.64 million atoms in motion, is more than six times larger than any biological simulations performed to date. The ribosome is the ancient molecular factory responsible for synthesizing proteins in all organisms. Using the new tool, the Los Alamos team led by Kevin Sanbonmatsu is the first to observe the entire ribosome in motion at atomic detail. This first simulation of the ribosome offers a new method for identifying potential antibiotic targets for such diseases as anthrax. Until now, only static, snapshot structures of the ribosome have been available. Science Daily, 11/01/2005.

Our role in this project is to develop force field for drug molecules, such as antibiotics paramomycin and tetracycline. This information will be used to study on atomic level how the drugs affect the protein-making function of the bacterial ribosome. This can help to identify potential candidates for more efficient and safe new antibiotics.

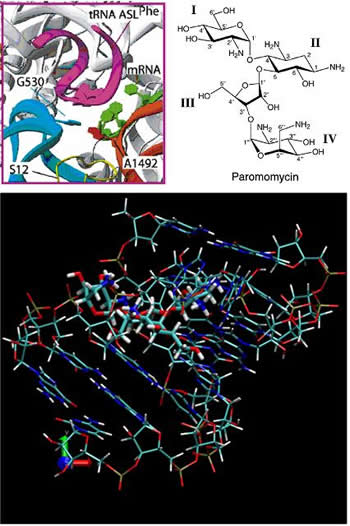
Figure 9: (on the right) Upper frames: Molecular environment of the decoding center of the ribosome (left) and chemical structure of the antibiotic paramomycin (right).

Lower frame: A computer model of paramomycin (bold) attached to the decoding center of the ribosome.

One way to explore a 3D PES is to plot a surface in space that connects all (x,y,z) points with the same value of energy V(x,y,z) - the iso-energy surface. Such a surface surrounds the 3D region allowed, classically, for molecular motion at a given value of energy in the molecule. It is instructive to prepare such surfaces for several values of energy and display them, one after another, in the order of increasing energy. I call this procedure the Energy Scan of the PES (ESPES). Examples, using hyper-spherical coordinates for triatomic molecules, follow.

• ESPES for ozone - Download PowerPoint
• ESPES for cyclic-N3 - Download PowerPoint

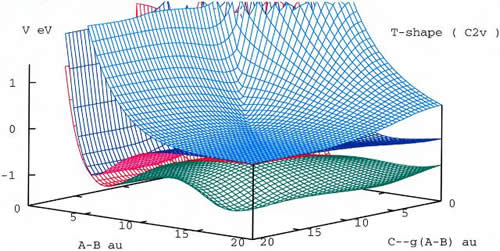
Figure 10: Three lowest adiabatic potential energy surfaces of Na3+ molecule. Only T-shaped configurations are shown in this picture. The avoided crossing seem between the two lowest states in the channel region and the conical intersection between the two upper states in equilateral configuration can be seen.